시계열 자료
. 시간의 흐름에 따라 관찰된 값들을 시계열 자료라 한다.
. 시계열 데이터의 분석을 통해 미래의 값을 예측하고 경향, 주기, 계절성 등을 파악하여 활용한다.
시계열 자료의 종류
1) 비정상성 시계열 자료
. 시계열 분석을 실시할 때 다루기 어려운 자료로 대부분의 시계열자료가 이에 해당한다.
2) 정상성 시계열 자료
. 비정상 시계열을 핸들링해 다루기 쉬운 시계열 자료로 변환한 자료이다.
정상성
평균이 일정할 경우
. 모든 시점에 대해 일정한 평균을 가진다.
. 평균이 일정하지 않은 시계열은 차분(difference)을 통해 정상화할 수 있다.
분산이 일정
. 분산도 시점에 의존하지 않고 일정해야 한다.
. 분산이 일정하지 않을 경우(Transformation)을 통해 정상화할 수 있다.
공분산도 단지 시차에만 의존, 실제특정시점 t, s에는 의존하지 않는다.
정상 시계열의 특징
. 정상 시계열은 어떤 시점에도 평균과 분산 그리고 특정한 시차의 길이를 갖는 자기공분산을 측정하더라도 동일한 값을 갖는다.
. 정상 시계열은 항상 그 평균값으로 회귀하려는 경향이 있으며, 그 평균값 주변에서의 변동은 대체로 일정한 폭을 갖는다.
.정상 시계열이 아닌 경우 특정 기간의 시계열 자료로부터 얻은 정보를 다른 시기로 일반화할 수 없다.
시계열자료 분석방법
분석방법
. 회귀분석(계량경제)방법, Box-Jenkins방법, 지수평활법, 시계열 분해법 등이 있다.
수학적 이론모형 : 회귀분석(계량경제)방법, Box-Jenkins방법
직관적 방법 : 지수평활법, 시계열 분해법으로 시간에 따른 변동이 느린 데이터 분석에 활용
장기 예측 : 회귀분석방법 활용
단기 예측 : Box-Jenkins방법, 지수평활법, 시계열 분해법 활용
자료 형태에 따른 분석방법
1) 일변량 시계열분석
. Box-Jenkins(ARMA), 지수평활법, 시계열 분해법 등이 있다.
.시간(t)을 설명변수로 한 회귀모형주가, 소매물가지수 등 하나의 변수에 관심을 갖는 경우의 시계열분석
2) 다중 시계열분석
.계량경제 모형, 전이함수 모형, 개입분석, 상태공간 분석, 다변량 ARIMA등
. 여러개의 시간(t)에 따른 변수들을 활용하는 시계열분삭
*계량경제(econometrics):시계열 데이터에 대한 회귀분석(예:이자율, 인플레이션이 환율에 미치는 요인)
이동평균법
이동평균법의 개념
. 과거로부터 현재까지의 시계열 자료를 대상으로 일정기간별 이동평균을 계산하고, 이들의 추세를 파악하여 다음 기간을 예측하는 방법
. 시계열 자료에서 계절변동과 불규칙변동을 제거하여 추세변동과 순환변동만 가진 시계열로 변환하는 방법으로도 사용됨

이동평균법의 특징
. 간단하고 쉽게 미래를 예측할 수 있으며, 자료의 수가 많고 안정된 패턴을 보이는 경우 예측의 품질(quality)가 높음.
. 특정 기간 안에 속하는 시계열에 대해서는 동일한 가중치를 부여함
. 일반적으로 시계열 자료에 뚜렷한 추세가 있거나 불규칙변동이 심하지 않은 경우에는 짧은 기간의 평균을 사요ㅛㅇ, 반대로 불규칙변동이 심한 경우 긴 기간의 평균을 사용함.
. 이동평균법에서 가장 중요한 것은 적절한 기간을 사용하는 것이다.
지수 평활법
지수평활법의 개념
. 일정기간의 평균을 이용하는 이동평균법과 달리 모든 시계열 자료를 사용하여 평균을 구하며, 시간의 흐름에 따라 최근 시계열에 더 많은 가중치를 부여하여 미래를 예측하는 방법.
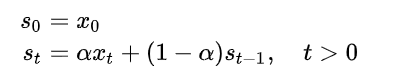
지수평활법의 특징
. 단기간에 발생하는 불규칙변동을 평활하는 방법
. 자료의 수가 많고, 안정된 패턴을 보이는 경우일수록 예측 품질이 높음
. 지수평활법에서 가중치의 역할을 하는 것은 지수평활계수(α)이며, 불규칙변동이 큰 시계열인 경우 지수평활계수는 작은 값을, 불규칙변동이 작은 시계열인 경우, 큰 값의 지수평활계수를 적용함(generally, α is between 0.05 and 0.3)
. 지수평활계수는 예측오차(실제 관측치와 예측치 사이의 잔차제곱합)을 비교하여 예측오차가 가장 작은 값을 선택하는 것이 바람직함
. 지수평활계수는 과거로 갈수록 지속적으로 감소한다
. 지수평활법은 불규칙변동의 영향을 제거하는 효과가 있으며, 중기 예측 이상에 주로 사용된다
시계열 모형
자기회귀모형(AR모형, autoregressvie model)
. p시점 전의 자료가 현재 자료에 영향을 주는 모형이다

. 자기상관함수(ACF)는 빠르게 감소, 부분자기함수(PACF)는 어느 시점에서 절단점을 가진다
자기상관함수
K 기간 떨어진 값들log(k)의 상관계수
부분(편)자기상관계수
. 서로 다른 두 시점 사이의 관계를 분석할 때 중간에 있는 값들의 영향을 제외시킨 상관관계 개념
이동평균 모형(MA모형, Moving Average model)
. 유한한 개수의 백색잡음의 결합이므로 언제나 정상성을 만족
. 1차 이동평균모형(MA1 모형)은 이동평균모형 중에서 가장 간단한 모형으로 시계열이 같은 시점의 백색잡음과 바로 전 시점의 백색잡음의 결합으로 이뤄진 모형
. AR 모형과 반대로 ACF에서 절단점을 갖고, PACF가 빠르게 감소

자기회귀누적이동평균 모형(ARIMA(p,d,q)모형, autoregressive integrated moving average model)
. ARIMA 모형은 비정상시계열 모형이다
. ARIMA 모형은 차분이나 변환을 통해 AR모형이나 MA모형, 이 둘을 합친 ARMA 모형으로 정상활 할 수 있다
. p는 AR모형, q는 MA모형과 관련이 있는 차수이다
분해 시계열
. 시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법을 말하며 회귀분석적인 방법을 주로 사용한다
* 영국 왕들의 사망 시 나이 데이터를 이용한 시계열분석
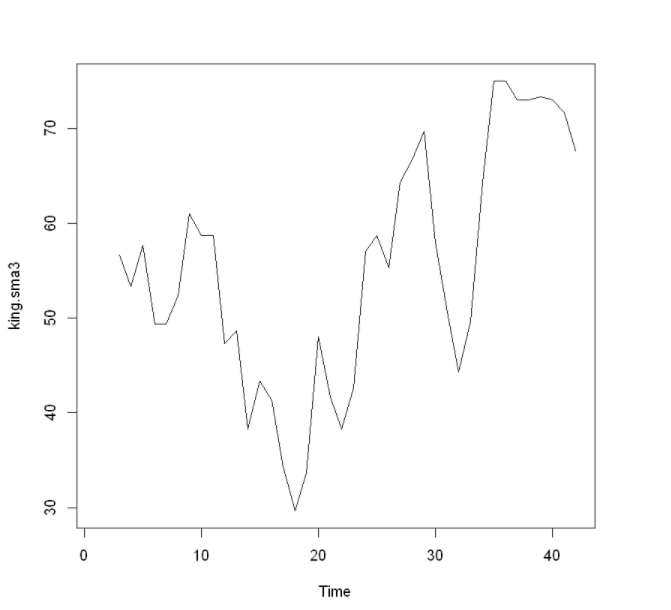
. 영국 왕 42명의 사망 시 나이 예제는 비계절성을 띄는 시계열 자료
. 비계절성을 띄는 시계열 자료는 트랜드 요소, 불규칙 요소로 구성
. 20번째 왕까지는 38세에서 55까지 수명을 유지하고, 그 이후부터는 수명이 늘어서 40번재 왕은 73세까지 생존
Rob J Hyndman
26 October 2020 research, ijf, forecasting There is a new call for papers for a special issue of the International Journal of Forecasting on “Innovations in hierarchical forecasting”. Guest editors: George Athanasopoulos, Rob J Hyndman, Anastasios Pana
robjhyndman.com





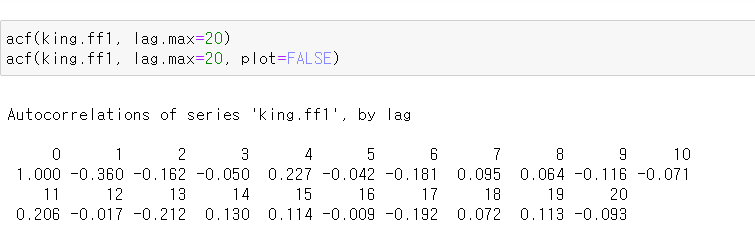


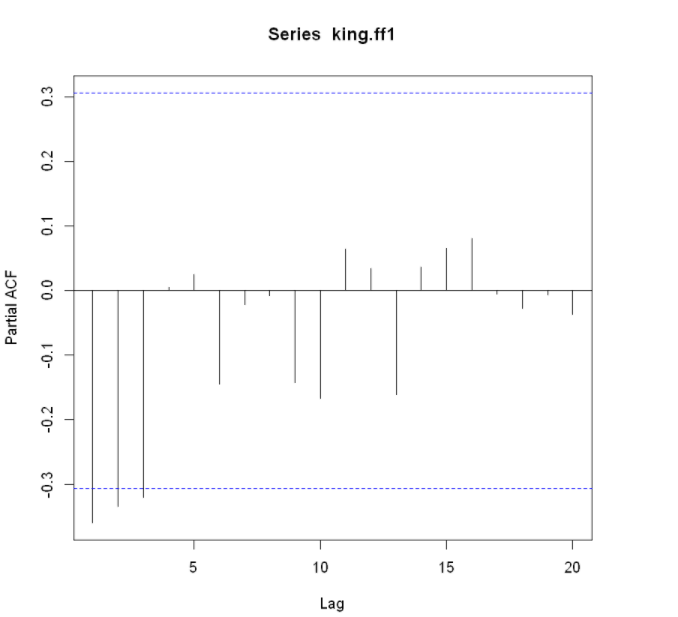
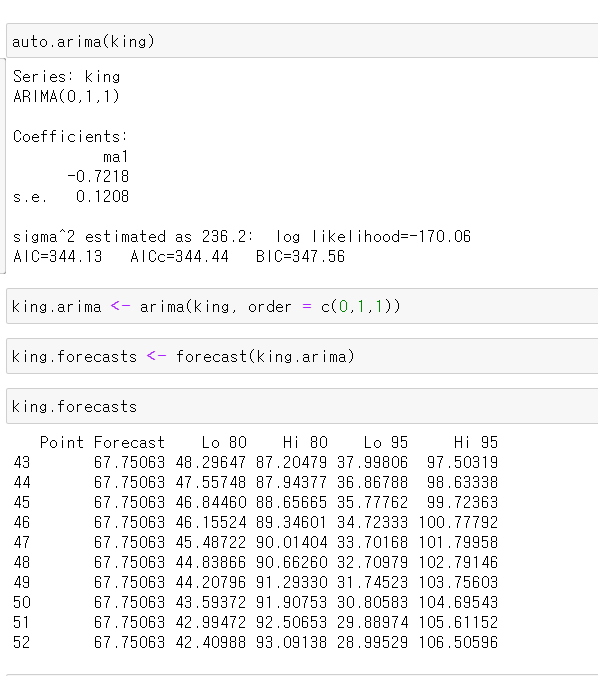
적절한 ARIMA 모형 찾기
영국 왕의 사망 나이 데이터의 적절한 ARIMA모형은 ARIMA(0,1,1)이다
'통계&확률' 카테고리의 다른 글
| T-test ,ANOVA-test 의 전제조건 (0) | 2021.04.08 |
|---|---|
| 다차원척도법(Multidimensional Scaling) (0) | 2021.03.12 |
| 통계분석 (0) | 2021.03.04 |
| 통계용어정리 (0) | 2021.02.14 |
| 통계용어 - 척도(scale) (0) | 2021.02.14 |